Predicting stock market trends using stochastic processes and probability theory
Fascination struck me one evening as I watched the stock market numbers dance up and down on my screen. It was not just a string of numbers, but a riddle begging to be solved. Could the key to this riddle lie in the world of mathematics and stochastic processes? This question turned into a personal challenge and set me on a path to explore the connection between stochastic processes, probability theory and stock market predictions. The investigation is motivated by an eagerness to understand and potentially predict market fluctuations using mathematical principles. The goal is simple: to dissect and apply statistical concepts to decipher patterns in financial developments. To this end, I intend to delve into probability models, which serve as the backbone of financial analysis, and explore how they can help predict market turns. For someone deeply fascinated by the intricacies of the financial world, the unpredictability of the stock market is not daunting; it is a puzzle to put together. This exploration reflects the convergence of my academic interests and personal inclinations – the tension of financial peaks and valleys framed by the orderliness of mathematical equations. Ultimately, the journey is both an intellectual endeavor and a personal venture aimed at uncovering whether stock market volatility is a language of randomness or one of predictable patterns, governed by the subtle laws of probability and stochastic processes.
Background information
Navigating the fluctuations of the stock market can often seem like a gamble, but it is supported by the solid foundation of probability theory and simple stochastic processes. As a high school student immersing myself in this subject, I have learned that probability fundamentally helps to understand uncertainty and measure how likely different outcomes are. This is particularly relevant in the stock market, where the outcome of an investment can be far from certain. One of the most fundamental ideas I have come across is the random walk theory. It suggests that stock prices move randomly and that each step, or price change, does not depend on the step before it. It’s like flipping a coin to determine whether a stock’s price should go up or down – each flip, like each day in the stock market, is independent of the last. But there is also a concept called mean reversion. This idea suggests that extreme fluctuations in stock prices are usually temporary and that prices tend to return to an average level over time. It is similar to how a stretched rubber band will eventually snap back into place. This return to normalcy can be an important consideration for investors given the timing of their trades. Another approach in the context of our curriculum is the analysis with Markov chains. These are sequences of events in which each event depends only on the state of the immediately preceding one. For example, if a company’s stock is doing well today, a Markov chain can be used to predict whether it will continue to do well tomorrow, completely independent of its performance last week. This helps simplify the complexity of market predictions by focusing on the present. Finally, we begin to touch on basic stochastic differential equations in our curriculum, which are equations with a random component that can evolve over time. Although the math can get sophisticated, the basic idea is that these equations can model stock prices by recognizing both their typical behavior and the random, unpredictable changes that can occur. These concepts, although complicated, can be broken down into high school math. They provide a toolbox for trying to understand and anticipate the often confusing trends in the stock market. By simplifying and applying these principles, I have begun to see how even the chaos of the financial world can reveal patterns and structure to those who know how to look for them.
Definition of
A stochastic process is basically a mathematical formula that helps us track random changes over time – think of it as a way of charting unpredictable ups and downs in stock prices. When we look at the stock market as a stochastic process, we focus on the unpredictable nature of how stock prices move, emphasizing the role of chance in their behavior. A martingale is a special type of stochastic process where, regardless of past trends, the expected future price of a stock is exactly its current price – much like how a fair coin toss gives you no clues about the next outcome. In stock market analysis, this suggests that predicting the direction of stock prices may be no easier than predicting a coin toss. The term “Markov chain” applies to sequences where each step depends only on the one immediately before it. For stock prices, this translates into the notion that predicting the next price relies solely on the current one without the need for historical prices. It’s like every decision depends only on the moment and does not take into account the past. Finally, Brownian motion describes a process in which changes occur continuously and randomly, much like the seemingly erratic movements of stock prices. This concept is central to financial theory because it forms the basis of various models that simulate stock price trajectories, helping analysts and investors to manage market uncertainty and quantify risk. Exploring these stochastic concepts provides us with a toolbox for examining and predicting market trends, linking mathematical probabilities with the seemingly random world of stock market fluctuations
Model building
Basic probability models
Exploring stock markets through the lens of mathematics begins with understanding probability distributions, particularly the normal distribution. This bell-shaped curve suggests that asset returns are most likely to be close to average, with extreme gains or losses being less common. Imagine this and envision the majority of stock returns clustering around the mean with fewer deviating far from it, showing the standard deviation, which tells us how spread out these returns are. This idea is useful because it suggests that wild swings in stock prices are not the norm; rather, they tend to gravitate towards their mean, allowing investors to anticipate returns within a certain range of normal fluctuations.
Random Walk Theory
Random Walk Theory paints stock price movements as unpredictable, similar to flipping a coin where previous flips have no bearing on the next outcome. Each price change, like each coin flip, is an independent event. This perspective challenges the ability to consistently predict market behavior because it asserts that the future direction of stock prices is as unknowable as predicting which side a coin will land on. This series of unpredictable steps suggests to analysts and investors alike that technical methods of prediction may not consistently outperform simple chance.
Brownian Motion for stock prices
Delving deeper into stock market modeling, Geometric Brownian Motion (GBM) becomes crucial. It refines Random Walk by taking into account the upward trend over time typical of stocks and their unpredictable fluctuations, known as volatility. GBM takes into account that stock returns compound over time and that changes in stock prices can be modeled to reflect their moving average returns along with randomness. This lends itself to simulating stock prices, providing a visual tool for understanding potential future stock behavior.
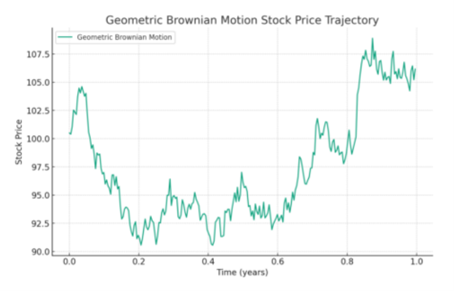
Black-Scholes models
Finally, the Black-Scholes model represents a cornerstone of option pricing, using the foundations of stochastic processes. It calculates the theoretical price of an option by balancing expected returns with the risk-free rate, under the assumption that market conditions are stable and risks are already embedded in current prices. Although the Black-Scholes assumptions were originally designed for option pricing, the assumptions can also be adapted to examine the predictability of the stock. By applying this model, we gain insight into stock trends under the principle that current prices reflect all known information, making future price movements based on historical data uncertain.
Experiment historical data analysis
In order to validate the theoretical models, I engaged in backtesting against historical stock market data. Using a sample of stocks in different sectors, I evaluated the performance of the Random Walk Theory, Mean-Reversion and Markov Chains models by comparing their output with actual stock prices over several years. The Random Walk model confirmed the unpredictability principle, with predictions similar to a coin toss in terms of accuracy. For Mean-Reversion, strategies centered around moving averages sometimes pointed out extreme price swings destined for correction. Markov Chain analysis, which narrowed the focus to immediate past prices, managed to adapt to short-term market movements, but struggled to predict over a longer timeline. Simulation with Geometric Brownian Motion To get a practical sense of how stocks might perform, I created simulations using Geometric Brownian Motion (GBM). I used an annualized return of 8%, consistent with historical averages, and a volatility rate reflecting historical fluctuations set at 15%, to generate hypothetical daily stock prices for a year. This created a spectrum of likely stock trajectories, providing a visual range of potential future market behaviors.
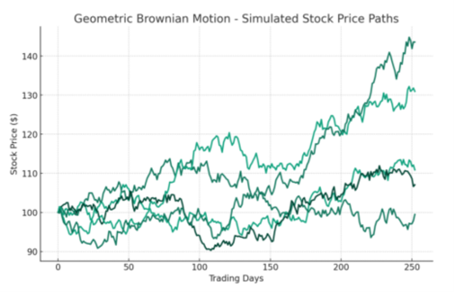
By plotting simulated price movements against actual historical data, some simulations proved to somewhat mirror the market, while others diverged. These differences confirmed the unpredictable nature of the stock market while demonstrating GBM’s ability to predict a possible range of stock prices rather than exact numbers. Evaluation of the Black-Scholes model When testing the Black-Scholes model, I used historical option prices and compared them to stock market prices to see how well the model could predict market trends. While the Black-Scholes model provided a benchmark for valuing options, it had difficulty predicting the direction of stocks due to its inherent limitations such as assuming constant volatility. Throughout the experiment, the theoretical models confronted the complex reality of the stock market. These trials not only pointed out the limitations of probability models in a live market context but also showcased their usefulness in offering an understanding of stock price behavior under certain conditions. Even amidst the unpredictability of the market, the experiment shed light on identifiable patterns through stochastic analysis.
Summary
Reflecting on the exploration of stochastic processes and probability theory, several insights emerge. The heart of this exploration lies in understanding the degree to which these mathematical tools can predict stock market trends – a conundrum wrapped in the volatility of financial markets. Starting with basic concepts such as the normal distribution, we have seen how stock returns tend to creep around a mean, offering predictability amidst randomness. The idea of stock movements as a random walk argues the opposite; market behavior occurs as a series of independent events, which challenges the ability to predict future prices based on historical data. In the realms of mean-reversion and Markov chains, we find a semblance of predictability. Mean-reversion suggests a gravitational pull of prices towards an average, hinting at when to trade, while Markov chains rely solely on the present to predict the future, avoiding the complexities of a stock’s history. These models insinuate conditional predictability into stock price movements. A more complex model, geometric Brownian Motion, provides a sophisticated simulation of stock price trajectories, which includes a long-term average upward trend and takes volatility into account. While this method beautifully reproduces potential paths that a stock might take, it again confirms that exact future values are elusive; rather, it outlines a range within which prices might oscillate. In the case of the Black-Scholes model, its skill in theoretical option pricing becomes apparent. But applying it to predict stock trends reveals its limitations, particularly the assumption of consistent volatility in an environment where change is the only constant. Each of these models reveals aspects of market behavior, but none stands as a crystal ball. Stochastic processes and probability theory delineate the contours of stock market trends and offer interpretable patterns within the apparent chaos. But this exploration also provides a sharp relief on the inherent unpredictability of financial markets. While these tools bring us closer to understanding market trends, they also teach us the importance of recognizing and managing the risks associated with trying to predict such a complex system. In conclusion, stochastic and probabilistic approaches have shed light on aspects of market predictability but also underscore the reality that the intricacies of the stock market cannot be fully captured by models alone. Above all, this study reinforces the conviction that while mathematics is a powerful ally in finance, market prediction remains an art as much as a science.
Reflection
The entry into the mathematical modeling of stock market trends reveals the delicate balance between theoretical elegance and practical applicability. A notable strength of these models, particularly the Geometric Brownian Motion (GBM), is how they distill complex market movements into comprehensible patterns, providing a framework for conceptualizing potential future behaviors of stock prices. GBM, for example, succeeds in outlining a ballpark for where stock prices might be in the future, which helps with risk assessment and portfolio management. However, the limitations are equally pronounced. The presumption of market efficiency embedded in these models, including the Black-Scholes model, can be overly simplistic. Markets often react violently to news or events that cannot be predicted by stochastic methods, indicating that aspects of human behavior and mass psychology are not captured by mathematical abstractions. This was evident as models sometimes failed to anticipate sharp market movements resulting from unexpected geopolitical or economic events. Moreover, the inherent assumption of a consistent level of volatility within the Black-Scholes model regularly faltered in the face of an erratic market. Market dynamics, such as sudden increases or decreases in stock prices, were not accurately predicted, suggesting that the models’ parameters need to be regularly recalibrated to reflect the changing market conditions. An unexpected finding was the extent to which some simplified models, such as the Markov chain, performed modestly well in predicting short-term price movements. Despite its simplicity, the model managed to capture some aspects of market behavior, underscoring the potential usefulness of less complex models under certain market conditions. In conclusion, although these mathematical models provide a solid starting point for understanding market trends, this exploration underscores their limitations, especially when applied outside theoretical contexts. The anomalies encountered reinforce the notion that models must be used in conjunction with an informed awareness of market realities, blurring the lines between quantitative analysis and qualitative assessment. The frontier of improving stock trend predictions could benefit greatly from the integration of advanced computational methods and the exploration of new stochastic models. Using machine learning can detect complex patterns within extensive financial data, providing a more nuanced forecast model than traditional methods. Moreover, considering stochastic volatility models that allow for dynamic changes in market volatility can provide a more accurate representation of financial markets than models that assume constant volatility. Looking at Levy processes, which capture sudden market movements, may also offer a more realistic picture of stock prices. Further research should tap into alternative data, such as social media sentiment and global economic indicators, to uncover new correlations that influence stock trends. Combining such data with insights from behavioral economics can provide a fuller picture of market drivers. Aiming for research that aligns these innovations into a coherent, predictive model could redefine the accuracy of market trend analysis. With a mix of cutting-edge technology, multifaceted modeling, and interdisciplinary studies, the potential to predict market trends could see significant progress.
About the Vikingen
With Vikingen’s signals, you have a good chance of finding the winners and selling in time. There are many securities. With Vikingen’s autopilots or tables, you can sort out the most interesting ETFs, stocks, options, warrants, funds, and so on. Vikingen is one of Sweden’s oldest equity research programs.
Click here to see what Vikingen offers: Detailed comparison – Stock market program for those who want to get even richer (vikingen.se)













