Interest on interest

Compound interest is an extremely important concept at all levels of finance. Compound interest can make a huge difference in the returns you get from your investments. As we know, simple interest is the act of earning interest on an investment. If you earned 10 percent on 100 kroner, you would get 10 kroner every year. On the other hand, with compound interest, that amount grows with the interest you receive. This is true for almost any investment nowadays, including your bank account. An example that is often used is the American Indian sale in Manhattan, New York for various items worth about $16. To many, that would seem like a very bad deal because $16 today is not worth much. But more than 400 years ago, it was a lot of money. If the American Indians had sold the items and invested the money at 8% interest on interest, they would not only have been able to buy back Manhattan today, but would have a very large amount of money left over. This is the real power of compound interest over longer periods of time. You may not have 400 years to save, but even over shorter time periods, compound interest will add up quickly. Let’s look at an analogy of planting trees that grow and produce other trees that would mimic a 10 percent compound interest. In this example, each tree will grow 10 percent of a new tree each year. Year 0: You have saved some money and managed to buy 10 trees and every 10 trees make one tree. Year 1: Next year you will have 11 trees Year 2: The year after that 12.1 trees Year 3: Then 13.3 trees Year 10: After ten years you will have 25.9 trees If this had been a simple interest rate there would only have been twenty trees. This may not seem like much, but if we look at the twenty-five year amount of investment on the compound interest versus simple interest, the compound interest would get 833 extra trees. If we look at this graphically, we can see the difference between the two even further.

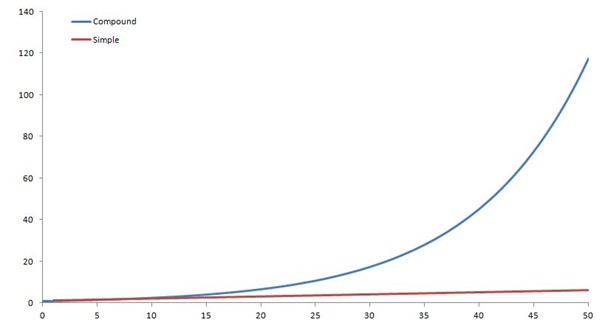We can see from the graph above that the composite yield curve looks a bit like a hockey stick. This will be true for any compound interest curve and is called an exponential curve. From here it is obvious that after 50 years, compound interest makes a very big difference.

Calculation

The calculation of compound interest is fairly simple but can become more complex when we start changing the compounding period. Here we will look at the basics of compounding once a year and calculating our interest once a year. A = P(l + R)t Example: If we have an interest rate of 5% and an investment of 100 crowns: Year 1: 105=100 (1+0.05)1 Year 2: 110.25=100 (1+0.05)2 Year 2: 115.76=100 (1+0.05)3 or Year 2: 110.25=105*(1+0.05) Year 3: 115.76=110.25*(1+0.05)

About the Vikingen

With Vikingen’s signals, you have a good chance of finding the winners and selling in time. There are many securities. With Vikingen’s autopilots or tables, you can sort out the most interesting ETFs, stocks, options, warrants, funds, and so on. Vikingen is one of Sweden’s oldest equity research programs.

Click here to see what Vikingen offers: Detailed comparison – Stock market program for those who want to get even richer (vikingen.se)