Forutsi trender i aksjemarkedet ved hjelp av stokastiske prosesser og sannsynlighetsteori

En kveld ble jeg fascinert da jeg så børstallene danse opp og ned på skjermen. Det var ikke bare en rekke tall, men en gåte som ba om å bli løst. Kunne nøkkelen til denne gåten ligge i matematikkens verden og i stokastiske prosesser? Dette spørsmålet ble til en personlig utfordring, og det satte meg på sporet av å utforske sammenhengen mellom stokastiske prosesser, sannsynlighetsteori og spådommer om aksjemarkedet. Undersøkelsen er motivert av en iver etter å forstå og potensielt forutsi markedssvingninger ved hjelp av matematiske prinsipper. Målet er enkelt: å dissekere og anvende statistiske konsepter for å tyde mønstre i den finansielle utviklingen. For å oppnå dette har jeg tenkt å fordype meg i sannsynlighetsmodeller, som utgjør ryggraden i finansiell analyse, og utforske hvordan de kan bidra til å forutsi markedssvingninger. For en som er dypt fascinert av finansverdenens forviklinger, er ikke uforutsigbarheten i aksjemarkedet avskrekkende; det er et puslespill å legge. Denne utforskningen gjenspeiler sammenfallet mellom mine akademiske interesser og personlige tilbøyeligheter – spenningen ved finansielle opp- og nedturer, innrammet av de matematiske ligningenes orden. Til syvende og sist er reisen både et intellektuelt og et personlig prosjekt som tar sikte på å avdekke om volatiliteten i aksjemarkedet er et språk for tilfeldigheter eller et språk for forutsigbare mønstre, styrt av de subtile lovene for sannsynlighet og stokastiske prosesser.

Bakgrunnsinformasjon

Å navigere i svingningene på aksjemarkedet kan ofte virke som et sjansespill, men det er støttet av et solid fundament av sannsynlighetsteori og enkle stokastiske prosesser. Som videregåendeelev har jeg fordypet meg i dette faget, og jeg har lært at sannsynlighetsteori i bunn og grunn hjelper oss å forstå usikkerhet og måle hvor sannsynlige ulike utfall er. Dette er særlig relevant i aksjemarkedet, der utfallet av en investering kan være langt fra sikkert. En av de mest grunnleggende ideene jeg har støtt på, er random walk-teorien. Den går ut på at aksjekursene beveger seg tilfeldig, og at hvert steg, eller hver kursendring, ikke avhenger av steget før det. Det er som å kaste mynt og kron for å avgjøre om en aksjekurs skal gå opp eller ned – hvert kast, akkurat som hver dag i aksjemarkedet, er uavhengig av det forrige. Men det finnes også et konsept som kalles mean reversion. Det går ut på at ekstreme svingninger i aksjekurser vanligvis er midlertidige, og at kursene har en tendens til å vende tilbake til et gjennomsnittsnivå over tid. Det kan sammenlignes med hvordan en strukket gummistrikk til slutt vil komme på plass igjen. Denne tilbakevendingen til det normale kan være viktig for investorer med tanke på timingen av deres handler. En annen tilnærming i forbindelse med pensumet vårt er analyse med Markov-kjeder. Dette er sekvenser av hendelser der hver hendelse kun avhenger av tilstanden til den umiddelbart foregående. Hvis for eksempel en aksje i et selskap gjør det bra i dag, kan en Markov-kjede brukes til å forutsi om den vil fortsette å gjøre det bra i morgen, helt uavhengig av hvordan det gikk i forrige uke. Dette bidrar til å forenkle kompleksiteten i markedsspådommer ved å fokusere på nåtiden. Til slutt begynner vi å berøre grunnleggende stokastiske differensialligninger i pensumet vårt, som er ligninger med en tilfeldig komponent som kan utvikle seg over tid. Selv om matematikken kan bli sofistikert, er grunntanken at disse ligningene kan modellere aksjekurser ved å ta hensyn til både deres typiske atferd og de tilfeldige, uforutsigbare endringene som kan oppstå. Selv om disse konseptene er kompliserte, kan de brytes ned til matematikk fra videregående skole. De gir en verktøykasse for å prøve å forstå og forutse de ofte forvirrende trendene i aksjemarkedet. Ved å forenkle og anvende disse prinsippene har jeg begynt å se hvordan selv kaoset i finansverdenen kan avsløre mønstre og struktur for dem som vet hvordan de skal se etter dem.

Definisjon

En stokastisk prosess er i bunn og grunn en matematisk formel som hjelper oss med å spore tilfeldige endringer over tid – tenk på det som en måte å kartlegge uforutsigbare opp- og nedturer i aksjekurser på. Når vi ser på aksjemarkedet som en stokastisk prosess, fokuserer vi på det uforutsigbare i hvordan aksjekursene beveger seg, og legger vekt på tilfeldighetenes rolle i utviklingen. En martingal er en spesiell type stokastisk prosess der den forventede fremtidige kursen på en aksje, uavhengig av tidligere trender, er nøyaktig den nåværende kursen – på samme måte som et rettferdig myntkast ikke gir deg noen ledetråder om det neste utfallet. I aksjemarkedsanalyse betyr dette at det kanskje ikke er enklere å forutsi aksjekursenes retning enn å forutsi et myntkast. Begrepet “Markov-kjede” brukes om sekvenser der hvert trinn kun avhenger av det som kommer umiddelbart før. For aksjekurser betyr dette at det å forutsi neste kurs kun avhenger av den nåværende kursen, uten at det er behov for historiske kurser. Det er som om hver beslutning bare avhenger av øyeblikket og ikke tar hensyn til fortiden. Til slutt beskriver Brownsk bevegelse en prosess der endringer skjer kontinuerlig og tilfeldig, omtrent som de tilsynelatende uberegnelige bevegelsene i aksjekursene. Dette konseptet er sentralt i finansteori fordi det danner grunnlaget for ulike modeller som simulerer aksjekursutviklingen, og som hjelper analytikere og investorer med å håndtere markedsusikkerhet og kvantifisere risiko. Ved å utforske disse stokastiske konseptene får vi en verktøykasse som gjør det mulig å undersøke og forutsi markedstrender ved å knytte matematiske sannsynligheter til den tilsynelatende tilfeldige verdenen av svingninger i aksjemarkedet

Modellbygging

Grunnleggende sannsynlighetsmodeller

Å utforske aksjemarkedene gjennom matematiske briller starter med å forstå sannsynlighetsfordelinger, særlig normalfordelingen. Denne klokkeformede kurven antyder at det er mest sannsynlig at avkastningen på aktiva ligger nær gjennomsnittet, mens ekstreme gevinster eller tap er mindre vanlige. Forestill deg dette og se for deg at de fleste aksjeavkastningene samler seg rundt gjennomsnittet, mens færre avviker langt fra det, og viser standardavviket, som forteller oss hvor spredt avkastningen er. Denne ideen er nyttig fordi den antyder at voldsomme svingninger i aksjekursene ikke er normen, men at de snarere har en tendens til å gravitere mot gjennomsnittet, slik at investorene kan forutse avkastningen innenfor et visst område av normale svingninger.

Teori om tilfeldige vandringer

Random Walk-teorien fremstiller aksjekursbevegelser som uforutsigbare, på samme måte som å kaste en mynt, der tidligere kast ikke har noen betydning for det neste utfallet. Hver kursendring, som hvert myntkast, er en uavhengig hendelse. Dette perspektivet utfordrer evnen til å forutsi markedsadferd på en konsistent måte, fordi det hevder at den fremtidige retningen på aksjekursene er like uviss som å forutsi hvilken side en mynt vil lande på. Denne serien av uforutsigbare trinn antyder for både analytikere og investorer at tekniske prediksjonsmetoder kanskje ikke alltid vil gi bedre resultater enn tilfeldigheter.

Brownsk bevegelse for aksjekurser

Når vi går dypere inn i modellering av aksjemarkedet, blir Geometrisk Brownsk Bevegelse (GBM) avgjørende. Den videreutvikler Random Walk ved å ta hensyn til den oppadgående trenden over tid som er typisk for aksjer, og deres uforutsigbare svingninger, kjent som volatilitet. GBM tar hensyn til at aksjeavkastningen er sammensatt over tid, og at endringer i aksjekurser kan modelleres slik at de gjenspeiler den glidende gjennomsnittsavkastningen sammen med tilfeldigheter. Dette egner seg godt til å simulere aksjekurser, og gir et visuelt verktøy for å forstå potensiell fremtidig aksjeadferd.

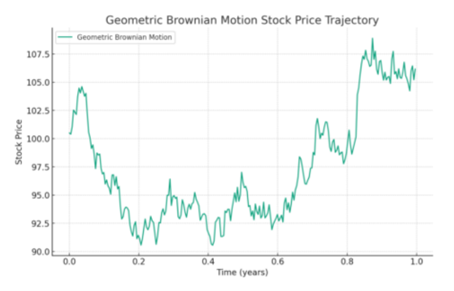
Black-Scholes-modeller

Black-Scholes-modellen er en hjørnestein i prisingen av opsjoner, og den bygger på stokastiske prosesser. Den beregner den teoretiske prisen på en opsjon ved å balansere forventet avkastning med den risikofrie renten, under forutsetning av at markedsforholdene er stabile og at risikoen allerede er innebygd i dagens priser. Selv om Black-Scholes-forutsetningene opprinnelig ble utviklet for opsjonsprising, kan forutsetningene også tilpasses for å undersøke forutsigbarheten til aksjen. Ved å bruke denne modellen får vi innsikt i aksjetrender under prinsippet om at dagens priser gjenspeiler all kjent informasjon, noe som gjør fremtidige kursbevegelser basert på historiske data usikre.

Analyse av historiske data fra eksperimentet

For å validere de teoretiske modellene har jeg gjennomført backtesting mot historiske aksjemarkedsdata. Ved hjelp av et utvalg aksjer i ulike sektorer evaluerte jeg resultatene til modellene Random Walk Theory, Mean-Reversion og Markov Chains ved å sammenligne resultatene deres med faktiske aksjekurser over flere år. Random Walk-modellen bekreftet uforutsigbarhetsprinsippet, med prediksjoner som var like treffsikre som et myntkast. For Mean-Reversion-modellen pekte strategier sentrert rundt glidende gjennomsnitt noen ganger ut ekstreme kurssvingninger som skulle korrigeres. Markov Chain-analysen, som begrenset fokuset til de siste kursene, klarte å tilpasse seg kortsiktige markedsbevegelser, men slet med å forutsi over en lengre tidslinje. Simulering med geometrisk Brownsk bevegelse For å få en praktisk følelse av hvordan aksjer kan utvikle seg, lagde jeg simuleringer ved hjelp av geometrisk Brownsk bevegelse (GBM). Jeg brukte en årlig avkastning på 8 %, i samsvar med historiske gjennomsnitt, og en volatilitetsrate som gjenspeiler historiske svingninger, satt til 15 %, for å generere hypotetiske daglige aksjekurser i ett år. Dette skapte et spekter av sannsynlige aksjekursbaner, noe som gir et visuelt bilde av potensiell fremtidig markedsadferd.

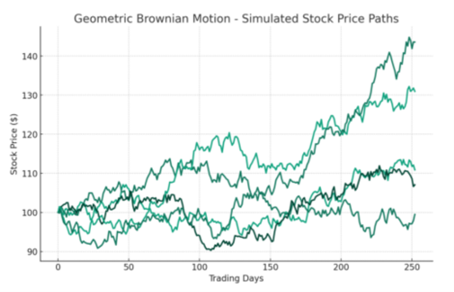
Ved å plotte simulerte kursbevegelser mot faktiske historiske data, viste det seg at noen simuleringer til en viss grad speilet markedet, mens andre avvek. Disse forskjellene bekreftet aksjemarkedets uforutsigbare natur, samtidig som de demonstrerte GBMs evne til å forutsi et mulig kursintervall snarere enn eksakte tall. Evaluering av Black-Scholes-modellen Da jeg testet Black-Scholes-modellen, brukte jeg historiske opsjonspriser og sammenlignet dem med aksjemarkedsprisene for å se hvor godt modellen kunne forutsi markedstrender. Selv om Black-Scholes-modellen ga en referanse for verdsettelse av opsjoner, hadde den problemer med å forutsi aksjemarkedets utvikling på grunn av sine iboende begrensninger, som for eksempel forutsetningen om konstant volatilitet. Gjennom hele eksperimentet ble de teoretiske modellene konfrontert med den komplekse virkeligheten i aksjemarkedet. Forsøkene viste ikke bare sannsynlighetsmodellenes begrensninger i en reell markedskontekst, men også hvor nyttige de er når det gjelder å forstå hvordan aksjekurser oppfører seg under visse betingelser. Selv midt i markedets uforutsigbarhet kastet eksperimentet lys over identifiserbare mønstre gjennom stokastisk analyse.

Sammendrag

Utforskningen av stokastiske prosesser og sannsynlighetsteori har gitt oss flere innsikter. Kjernen i denne utforskningen ligger i å forstå i hvilken grad disse matematiske verktøyene kan forutsi trender i aksjemarkedet – en gåte som er knyttet til volatiliteten i finansmarkedene. Med utgangspunkt i grunnleggende begreper som normalfordelingen har vi sett hvordan aksjeavkastningen har en tendens til å krype rundt et gjennomsnitt, noe som gir forutsigbarhet midt i tilfeldighetene. Tanken om aksjebevegelser som en “random walk” argumenterer for det motsatte; markedsatferd oppstår som en serie uavhengige hendelser, noe som utfordrer evnen til å forutsi fremtidige priser basert på historiske data. I middelverdi-reversering og Markov-kjeder finner vi et skinn av forutsigbarhet. Mean-reversion antyder en gravitasjon som trekker kursene mot et gjennomsnitt, noe som gir en pekepinn om når man bør handle, mens Markov-kjeder utelukkende baserer seg på nåtiden for å forutsi fremtiden, og unngår kompleksiteten i en aksjes historie. Disse modellene gir betinget forutsigbarhet i aksjekursbevegelsene. En mer kompleks modell, geometrisk Brownsk bevegelse, gir en sofistikert simulering av aksjekursbaner, som inkluderer en langsiktig gjennomsnittlig oppadgående trend og tar hensyn til volatilitet. Selv om denne metoden på en vakker måte gjengir potensielle baner som en aksje kan ta, bekrefter den igjen at eksakte fremtidige verdier er vanskelig å få tak i. Den skisserer snarere et intervall som kursene kan svinge innenfor. Når det gjelder Black-Scholes-modellen, blir dens dyktighet innen teoretisk opsjonsprising tydelig. Men når den brukes til å forutsi aksjetrender, avslører den sine begrensninger, særlig forutsetningen om konstant volatilitet i et miljø der endring er den eneste konstanten. Hver av disse modellene avslører aspekter ved markedsatferden, men ingen av dem kan brukes som krystallkule. Stokastiske prosesser og sannsynlighetsteori tegner konturene av trendene i aksjemarkedet og tilbyr tolkbare mønstre i det tilsynelatende kaoset. Men denne utforskningen gir også et skarpt bilde av finansmarkedenes iboende uforutsigbarhet. Selv om disse verktøyene bringer oss nærmere en forståelse av markedstrendene, lærer de oss også hvor viktig det er å erkjenne og håndtere risikoen forbundet med å forsøke å forutsi et så komplekst system. Konklusjonen er at stokastiske og probabilistiske tilnærminger har kastet lys over aspekter ved markedets forutsigbarhet, men de understreker også at aksjemarkedets forviklinger ikke fullt ut kan fanges opp av modeller alene. Fremfor alt styrker denne studien troen på at selv om matematikken er en mektig alliert i finansverdenen, er markedsprediksjon like mye en kunst som en vitenskap.

Refleksjon

Den matematiske modelleringen av trender i aksjemarkedet avslører den hårfine balansen mellom teoretisk eleganse og praktisk anvendelighet. En bemerkelsesverdig styrke ved disse modellene, særlig Geometrisk Brownsk Bevegelse (GBM), er hvordan de destillerer komplekse markedsbevegelser til forståelige mønstre, noe som gir et rammeverk for å konseptualisere potensiell fremtidig atferd i aksjekursene. GBM lykkes for eksempel med å skissere et bilde av hvor aksjekursene kan befinne seg i fremtiden, noe som er til hjelp ved risikovurdering og porteføljeforvaltning. Begrensningene er imidlertid like uttalte. Antakelsen om markedseffisiens som ligger i disse modellene, inkludert Black-Scholes-modellen, kan være altfor forenklet. Markedene reagerer ofte voldsomt på nyheter eller hendelser som ikke kan forutsies ved hjelp av stokastiske metoder, noe som tyder på at aspekter ved menneskelig atferd og massepsykologi ikke lar seg fange opp av matematiske abstraksjoner. Dette ble tydelig da modellene noen ganger ikke klarte å forutsi kraftige markedsbevegelser som følge av uventede geopolitiske eller økonomiske hendelser. Dessuten sviktet Black-Scholes-modellens iboende antakelse om et konstant volatilitetsnivå regelmessig i møte med et uberegnelig marked. Markedsdynamikk, som plutselige økninger eller fall i aksjekursene, ble ikke forutsagt nøyaktig, noe som tyder på at modellenes parametere jevnlig må rekalibreres for å gjenspeile de skiftende markedsforholdene. Et uventet funn var i hvilken grad noen forenklede modeller, som Markov-kjeden, presterte beskjedent godt når det gjaldt å forutsi kortsiktige kursbevegelser. Til tross for sin enkelhet klarte modellen å fange opp noen aspekter ved markedsatferden, noe som understreker den potensielle nytten mindre komplekse modeller kan ha under visse markedsforhold. Selv om disse matematiske modellene gir et solid utgangspunkt for å forstå markedstrender, understreker denne undersøkelsen at de har sine begrensninger, særlig når de brukes utenfor teoretiske sammenhenger. De avvikene vi har sett, forsterker oppfatningen om at modeller må brukes sammen med en informert bevissthet om markedsrealiteter, og at grensene mellom kvantitativ analyse og kvalitativ vurdering må viskes ut. For å forbedre prediksjonene av aksjetrender kan vi dra stor nytte av å integrere avanserte beregningsmetoder og utforske nye stokastiske modeller. Maskinlæring kan oppdage komplekse mønstre i omfattende finansielle data, noe som gir en mer nyansert prognosemodell enn tradisjonelle metoder. Dessuten kan stokastiske volatilitetsmodeller som tar høyde for dynamiske endringer i markedsvolatiliteten, gi en mer nøyaktig representasjon av finansmarkedene enn modeller som forutsetter konstant volatilitet. Levy-prosesser, som fanger opp plutselige markedsbevegelser, kan også gi et mer realistisk bilde av aksjekursene. Videre forskning bør ta i bruk alternative data, for eksempel stemningsdata fra sosiale medier og globale økonomiske indikatorer, for å avdekke nye korrelasjoner som påvirker aksjetrender. Ved å kombinere slike data med innsikt fra atferdsøkonomi kan man få et mer utfyllende bilde av markedsdriverne. Forskning som setter disse nyvinningene sammen til en sammenhengende, prediktiv modell, kan omdefinere nøyaktigheten i analyser av markedstrender. Med en blanding av banebrytende teknologi, mangefasettert modellering og tverrfaglige studier kan potensialet for å forutsi markedstrender øke betraktelig.

Om Vikingen

Med Vikingens signaler har du god sjanse til å finne vinnerne og selge i tide. Det er mange verdipapirer. Med Vikingens autopiloter eller tabeller kan du sortere ut de mest interessante ETFene, aksjene, opsjonene, warrantene, fondene m.m. Vikingen er et av Sveriges eldste aksjeanalyseprogrammer.

Klikk her for å se hva Vikingen tilbyr: Detaljert sammenligning – Børsprogram for de som ønsker å bli enda rikere (vikingen.se)