Forudsigelse af tendenser på aktiemarkedet ved hjælp af stokastiske processer og sandsynlighedsteori

En aften blev jeg fascineret, da jeg så tallene på aktiemarkedet danse op og ned på min skærm. Det var ikke bare en række tal, men en gåde, der tiggede om at blive løst. Kunne nøglen til denne gåde ligge i matematikkens verden og i stokastiske processer? Dette spørgsmål blev til en personlig udfordring og satte mig i gang med at udforske forbindelsen mellem stokastiske processer, sandsynlighedsteori og forudsigelser af aktiemarkedet. Undersøgelsen er motiveret af en iver efter at forstå og potentielt forudsige markedsudsving ved hjælp af matematiske principper. Målet er enkelt: at dissekere og anvende statistiske begreber til at dechifrere mønstre i den finansielle udvikling. Til det formål vil jeg dykke ned i sandsynlighedsmodeller, som er rygraden i finansiel analyse, og undersøge, hvordan de kan hjælpe med at forudsige markedssvingninger. For en person, der er dybt fascineret af den finansielle verdens forviklinger, er aktiemarkedets uforudsigelighed ikke skræmmende; det er et puslespil, der skal lægges. Denne udforskning afspejler konvergensen mellem mine akademiske interesser og personlige tilbøjeligheder – spændingen ved finansielle toppe og bunde indrammet af de matematiske ligningers orden. I sidste ende er rejsen både en intellektuel bestræbelse og et personligt foretagende, der har til formål at afsløre, om volatiliteten på aktiemarkedet er et sprog for tilfældighed eller et sprog for forudsigelige mønstre, der styres af de subtile love for sandsynlighed og stokastiske processer.

Baggrundsinformation

At navigere i aktiemarkedets udsving kan ofte virke som et sats, men det understøttes af et solidt fundament af sandsynlighedsteori og simple stokastiske processer. Som gymnasieelev, der fordyber sig i dette fag, har jeg lært, at sandsynlighed grundlæggende hjælper med at forstå usikkerhed og måle, hvor sandsynlige forskellige udfald er. Det er især relevant på aktiemarkedet, hvor udfaldet af en investering langt fra kan være sikkert. En af de mest grundlæggende ideer, jeg er stødt på, er random walk-teorien. Den går ud på, at aktiekurserne bevæger sig tilfældigt, og at hvert trin eller hver prisændring ikke afhænger af det foregående trin. Det er som at kaste en mønt for at afgøre, om en aktiekurs skal gå op eller ned – hvert kast, ligesom hver dag på aktiemarkedet, er uafhængigt af det sidste. Men der er også et begreb, der hedder mean reversion. Denne idé går ud på, at ekstreme udsving i aktiekurserne normalt er midlertidige, og at kurserne har en tendens til at vende tilbage til et gennemsnitligt niveau over tid. Det svarer til, at en udspændt elastik til sidst vil falde på plads igen. Denne tilbagevenden til normalitet kan være en vigtig overvejelse for investorer i betragtning af timingen af deres handler. En anden tilgang i forbindelse med vores pensum er analysen med Markov-kæder. Det er sekvenser af begivenheder, hvor hver begivenhed kun afhænger af tilstanden i den umiddelbart foregående. Hvis det f.eks. går godt for en virksomheds aktier i dag, kan en Markov-kæde bruges til at forudsige, om det fortsat vil gå godt i morgen, helt uafhængigt af, hvordan det gik i sidste uge. Dette hjælper med at forenkle kompleksiteten i markedsforudsigelser ved at fokusere på nutiden. Endelig begynder vi at berøre grundlæggende stokastiske differentialligninger i vores pensum, som er ligninger med en tilfældig komponent, der kan udvikle sig over tid. Selvom matematikken kan blive sofistikeret, er den grundlæggende idé, at disse ligninger kan modellere aktiekurser ved at anerkende både deres typiske adfærd og de tilfældige, uforudsigelige ændringer, der kan forekomme. Selv om disse begreber er komplicerede, kan de nedbrydes til gymnasiematematik. De giver en værktøjskasse til at forsøge at forstå og forudse de ofte forvirrende tendenser på aktiemarkedet. Ved at forenkle og anvende disse principper er jeg begyndt at se, hvordan selv kaos i finansverdenen kan afsløre mønstre og struktur for dem, der ved, hvordan de skal lede efter dem.

Definition

En stokastisk proces er dybest set en matematisk formel, der hjælper os med at spore tilfældige ændringer over tid – tænk på det som en måde at kortlægge uforudsigelige op- og nedture i aktiekurserne. Når vi ser på aktiemarkedet som en stokastisk proces, fokuserer vi på den uforudsigelige karakter af, hvordan aktiekurserne bevæger sig, og understreger tilfældighedernes rolle i deres adfærd. En martingal er en særlig type stokastisk proces, hvor den forventede fremtidige pris på en aktie, uanset tidligere tendenser, er præcis den nuværende pris – ligesom et fair møntkast ikke giver dig noget fingerpeg om det næste resultat. I aktiemarkedsanalyse antyder dette, at det måske ikke er nemmere at forudsige retningen på aktiekurserne end at forudsige et møntkast. Udtrykket “Markov-kæde” gælder for sekvenser, hvor hvert trin kun afhænger af det, der kommer umiddelbart før. For aktiekurser betyder det, at forudsigelsen af den næste pris udelukkende afhænger af den nuværende uden behov for historiske priser. Det er, som om enhver beslutning kun afhænger af øjeblikket og ikke tager højde for fortiden. Endelig beskriver Brownsk bevægelse en proces, hvor ændringer sker kontinuerligt og tilfældigt, ligesom de tilsyneladende uberegnelige bevægelser i aktiekurserne. Dette begreb er centralt i finansiel teori, fordi det danner grundlag for forskellige modeller, der simulerer aktiekursernes udvikling og hjælper analytikere og investorer med at styre usikkerheden på markedet og kvantificere risikoen. Ved at udforske disse stokastiske begreber får vi en værktøjskasse til at undersøge og forudsige markedstendenser ved at forbinde matematiske sandsynligheder med den tilsyneladende tilfældige verden af udsving på aktiemarkedet.

Opbygning af modeller

Grundlæggende sandsynlighedsmodeller

At udforske aktiemarkederne gennem matematikkens briller starter med at forstå sandsynlighedsfordelinger, især normalfordelingen. Denne klokkeformede kurve antyder, at afkast på aktiver højst sandsynligt vil ligge tæt på gennemsnittet, mens ekstreme gevinster eller tab er mindre almindelige. Forestil dig dette og forestil dig, at størstedelen af aktieafkastene samler sig omkring gennemsnittet, mens færre afviger langt fra det, hvilket viser standardafvigelsen, som fortæller os, hvor spredte disse afkast er. Denne idé er nyttig, fordi den antyder, at vilde udsving i aktiekurserne ikke er normen; de har snarere en tendens til at bevæge sig mod deres gennemsnit, hvilket giver investorer mulighed for at forvente afkast inden for et vist interval af normale udsving.

Teori om tilfældige vandringer

Random Walk-teorien beskriver aktiekursbevægelser som uforudsigelige, ligesom når man kaster en mønt, hvor tidligere kast ikke har nogen betydning for det næste resultat. Hver kursændring er, ligesom hvert møntkast, en uafhængig begivenhed. Dette perspektiv udfordrer evnen til konsekvent at forudsige markedsadfærd, fordi det hævder, at aktiekursernes fremtidige retning er lige så uvis som at forudsige, hvilken side en mønt vil lande på. Denne række af uforudsigelige trin antyder for både analytikere og investorer, at tekniske forudsigelsesmetoder måske ikke konsekvent overgår simple tilfældigheder.

Brownsk bevægelse for aktiekurser

Hvis man dykker dybere ned i modellering af aktiemarkedet, bliver Geometric Brownian Motion (GBM) afgørende. Den forfiner Random Walk ved at tage højde for den opadgående tendens over tid, der er typisk for aktier, og deres uforudsigelige udsving, kendt som volatilitet. GBM tager højde for, at aktieafkast sammensættes over tid, og at ændringer i aktiekurser kan modelleres til at afspejle deres glidende gennemsnitsafkast sammen med tilfældighed. Dette egner sig til at simulere aktiekurser og giver et visuelt værktøj til at forstå potentiel fremtidig aktieadfærd.

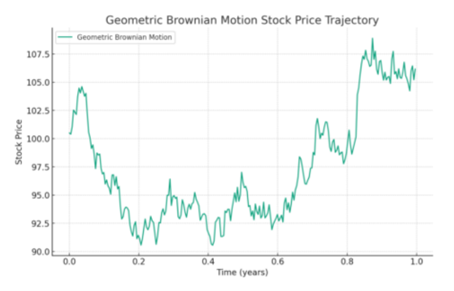
Black-Scholes-modeller

Endelig repræsenterer Black-Scholes-modellen en hjørnesten i prisfastsættelsen af optioner ved hjælp af grundlaget for stokastiske processer. Den beregner den teoretiske pris på en option ved at afveje det forventede afkast med den risikofrie rente under antagelse af, at markedsforholdene er stabile, og at risici allerede er indlejret i de aktuelle priser. Selvom Black-Scholes-antagelserne oprindeligt blev designet til prisfastsættelse af optioner, kan antagelserne også tilpasses til at undersøge aktiens forudsigelighed. Ved at anvende denne model får vi indsigt i aktietrends ud fra princippet om, at de aktuelle priser afspejler alle kendte oplysninger, hvilket gør fremtidige prisbevægelser baseret på historiske data usikre.

Analyse af eksperimentets historiske data

For at validere de teoretiske modeller foretog jeg backtesting på baggrund af historiske aktiemarkedsdata. Ved hjælp af et udvalg af aktier i forskellige sektorer evaluerede jeg resultaterne af modellerne Random Walk Theory, Mean-Reversion og Markov Chains ved at sammenligne deres output med de faktiske aktiekurser over flere år. Random Walk-modellen bekræftede uforudsigelighedsprincippet med forudsigelser, der svarer til et møntkast med hensyn til nøjagtighed. For Mean-Reversion pegede strategier centreret omkring glidende gennemsnit nogle gange på ekstreme kurssvingninger, der var bestemt til korrektion. Markov-kædeanalyse, som indsnævrede fokus til umiddelbare tidligere priser, formåede at tilpasse sig kortsigtede markedsbevægelser, men havde svært ved at forudsige over en længere tidslinje. Simulering med Geometric Brownian Motion For at få en praktisk fornemmelse af, hvordan aktier kan klare sig, lavede jeg simuleringer med Geometric Brownian Motion (GBM). Jeg brugte et årligt afkast på 8 % i overensstemmelse med historiske gennemsnit og en volatilitetsrate, der afspejler historiske udsving, på 15 % til at generere hypotetiske daglige aktiekurser i et år. Dette skabte et spektrum af sandsynlige aktiekurser, som giver et visuelt billede af den potentielle fremtidige markedsadfærd.

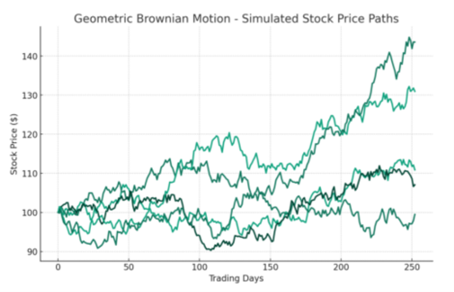
Ved at sammenligne simulerede kursbevægelser med faktiske historiske data viste det sig, at nogle simuleringer i nogen grad afspejlede markedet, mens andre afveg. Disse forskelle bekræftede aktiemarkedets uforudsigelige natur og demonstrerede samtidig GBM’s evne til at forudsige et muligt interval af aktiekurser snarere end nøjagtige tal. Evaluering af Black-Scholes-modellen Da jeg testede Black-Scholes-modellen, brugte jeg historiske optionspriser og sammenlignede dem med aktiemarkedspriserne for at se, hvor godt modellen kunne forudsige markedstendenser. Mens Black-Scholes-modellen gav et benchmark for værdiansættelse af optioner, havde den svært ved at forudsige aktiernes retning på grund af dens iboende begrænsninger som f.eks. antagelsen om konstant volatilitet. Under hele eksperimentet blev de teoretiske modeller konfronteret med den komplekse virkelighed på aktiemarkedet. Disse forsøg påpegede ikke kun sandsynlighedsmodellernes begrænsninger i en levende markedssammenhæng, men viste også deres anvendelighed til at give en forståelse af aktiekursens adfærd under visse forhold. Selv midt i markedets uforudsigelighed kastede eksperimentet lys over identificerbare mønstre gennem stokastisk analyse.

Sammenfatning

Når man reflekterer over udforskningen af stokastiske processer og sandsynlighedsteori, dukker der flere indsigter op. Kernen i denne udforskning ligger i at forstå, i hvor høj grad disse matematiske værktøjer kan forudsige tendenser på aktiemarkedet – en gåde, der er indhyllet i finansmarkedernes volatilitet. Med udgangspunkt i grundlæggende begreber som normalfordelingen har vi set, hvordan aktieafkast har en tendens til at krybe omkring et gennemsnit, hvilket giver forudsigelighed midt i tilfældigheden. Ideen om aktiebevægelser som en random walk argumenterer for det modsatte; markedsadfærd opstår som en række uafhængige begivenheder, hvilket udfordrer evnen til at forudsige fremtidige priser baseret på historiske data. I forbindelse med mean-reversion og Markov-kæder finder vi en form for forudsigelighed. Mean-reversion antyder, at priserne trækker mod et gennemsnit, hvilket giver et fingerpeg om, hvornår man skal handle, mens Markov-kæder udelukkende baserer sig på nutiden for at forudsige fremtiden og dermed undgår kompleksiteten i en akties historie. Disse modeller indfører betinget forudsigelighed i aktiekursbevægelser. En mere kompleks model, geometrisk Brownsk bevægelse, giver en sofistikeret simulering af aktiekursbaner, som inkluderer en langsigtet gennemsnitlig opadgående tendens og tager højde for volatilitet. Selv om denne metode smukt gengiver potentielle veje, som en aktie kan tage, bekræfter den igen, at nøjagtige fremtidige værdier er uhåndgribelige; den skitserer snarere et interval, inden for hvilket priserne kan svinge. Når det gælder Black-Scholes-modellen, bliver dens dygtighed inden for teoretisk optionsprisfastsættelse tydelig. Men når den anvendes til at forudsige aktietrends, afsløres dens begrænsninger, især antagelsen om konstant volatilitet i et miljø, hvor forandring er den eneste konstant. Hver af disse modeller afslører aspekter af markedsadfærd, men ingen er en krystalkugle. Stokastiske processer og sandsynlighedsteori aftegner konturerne af aktiemarkedets tendenser og tilbyder fortolkelige mønstre i det tilsyneladende kaos. Men denne udforskning giver også et skarpt billede af finansmarkedernes iboende uforudsigelighed. Mens disse værktøjer bringer os tættere på en forståelse af markedstendenser, lærer de os også vigtigheden af at anerkende og styre de risici, der er forbundet med at forsøge at forudsige et så komplekst system. Konklusionen er, at stokastiske og probabilistiske tilgange har kastet lys over aspekter af markedets forudsigelighed, men også understreget, at aktiemarkedets forviklinger ikke kan indfanges fuldt ud af modeller alene. Frem for alt styrker denne undersøgelse troen på, at selv om matematik er en stærk allieret i finansverdenen, er markedsforudsigelse lige så meget en kunst som en videnskab.

Refleksion

Indgangen til den matematiske modellering af aktiemarkedstendenser afslører den skrøbelige balance mellem teoretisk elegance og praktisk anvendelighed. En bemærkelsesværdig styrke ved disse modeller, især den geometriske brownske bevægelse (GBM), er, hvordan de destillerer komplekse markedsbevægelser til forståelige mønstre og giver en ramme for konceptualisering af aktiekursernes potentielle fremtidige adfærd. GBM er f.eks. i stand til at skitsere, hvor aktiekurserne kan befinde sig i fremtiden, hvilket hjælper med risikovurdering og porteføljestyring. Begrænsningerne er dog lige så udtalte. Antagelsen om markedseffektivitet, som er indlejret i disse modeller, herunder Black-Scholes-modellen, kan være alt for forenklet. Markederne reagerer ofte voldsomt på nyheder eller begivenheder, som ikke kan forudsiges ved hjælp af stokastiske metoder, hvilket viser, at aspekter af menneskelig adfærd og massepsykologi ikke kan indfanges af matematiske abstraktioner. Det var tydeligt, da modellerne nogle gange ikke kunne forudsige skarpe markedsbevægelser som følge af uventede geopolitiske eller økonomiske begivenheder. Desuden svigtede den iboende antagelse om et ensartet volatilitetsniveau i Black-Scholes-modellen regelmæssigt i forhold til et uberegneligt marked. Markedsdynamik, såsom pludselige stigninger eller fald i aktiekurserne, blev ikke forudsagt præcist, hvilket tyder på, at modellernes parametre regelmæssigt skal rekalibreres for at afspejle de skiftende markedsforhold. Et uventet resultat var, at nogle forenklede modeller, såsom Markov-kæden, klarede sig beskedent godt i forhold til at forudsige kortsigtede prisbevægelser. På trods af deres enkelhed lykkedes det modellen at indfange nogle aspekter af markedsadfærden, hvilket understreger den potentielle anvendelighed af mindre komplekse modeller under visse markedsforhold. Konklusionen er, at selvom disse matematiske modeller giver et solidt udgangspunkt for at forstå markedstendenser, understreger denne undersøgelse deres begrænsninger, især når de anvendes uden for teoretiske sammenhænge. De uregelmæssigheder, der er fundet, forstærker opfattelsen af, at modeller skal bruges sammen med en informeret bevidsthed om markedsrealiteter, hvilket slører grænserne mellem kvantitativ analyse og kvalitativ vurdering. Forbedring af forudsigelser af aktietendenser kan i høj grad drage fordel af integrationen af avancerede beregningsmetoder og udforskningen af nye stokastiske modeller. Maskinlæring kan opdage komplekse mønstre i omfattende finansielle data og give en mere nuanceret prognosemodel end traditionelle metoder. Desuden kan stokastiske volatilitetsmodeller, der tager højde for dynamiske ændringer i markedsvolatiliteten, give en mere præcis repræsentation af finansmarkederne end modeller, der antager konstant volatilitet. At se på Levy-processer, som indfanger pludselige markedsbevægelser, kan også give et mere realistisk billede af aktiekurserne. Yderligere forskning bør udnytte alternative data, som f.eks. stemningen på de sociale medier og globale økonomiske indikatorer, for at afdække nye sammenhænge, der påvirker aktietrends. Ved at kombinere sådanne data med indsigter fra adfærdsøkonomi kan man få et mere fuldstændigt billede af markedets drivkræfter. At sigte mod forskning, der tilpasser disse innovationer til en sammenhængende, forudsigelig model, kan omdefinere nøjagtigheden af analyser af markedstendenser.

Med en blanding af banebrydende teknologi, mangefacetteret modellering og tværfaglige undersøgelser kan der ske store fremskridt med hensyn til at forudsige markedstendenser.

Om Vikingen

Med Vikingens signaler har du en god chance for at finde vinderne og sælge i tide. Der findes mange værdipapirer. Med Vikingens autopiloter eller tabeller kan du sortere de mest interessante ETF’er, aktier, optioner, warrants, fonde og så videre. Vikingen er et af Sveriges ældste aktieanalyseprogrammer.

Klik her for at se, hvad Vikingen tilbyder: Detaljeret sammenligning – Aktiemarkedsprogram for dig, der vil være endnu rigere (vikingen.se)