Standard avvikelse (Volatilitet)

Beskrivning:

Grundidén är att marknaden når en botten vid panikförsäljning, efter vilken, en rekyl uppåt tar vid. Detta kan man mäta med standard avvikelsen.

Standard avvikelse är en statistisk term som förser oss med en god indikation på volatiliteten i en aktie.
Den mäter hur långt kursen avviker från medelkursen. Ju större avvikelse slutkursen har från medelkursen, ju högre är volatiliteten och tvärtom. Ofta beräknar man standardavvikelsen på 20 dagar eftersom det representerar en vanlig månad.

Tolkning:

Volatilitet har flera användningsområden.

För det första: Storleken (hög, låg) på volatiliteten kan användas för att bestämma om en aktie skall väljas eller inte. Låg volatilitet i en aktie antyder att aktien har förmåga att hålla sig vid sin underliggande trend medan en hög volatilitet antyder att aktien har förmågan att sticka iväg från sin underliggande trend, åt båda hållen, så att det till slut inte finns någon trend att följa i det korta perspektivet. Hög risk alltså. På så sätt kan man avgöra om en aktie ska betraktas som kort eller lång investering innan man stiger in i den.

För det andra: När en aktie tycks ha fastnat inom ett viss område av volatilitet och sedan bryter ut ur området uppåt, kan det betyda att trenden kommer att vända. Om den bryter ut nedåt kan det betyda att antalet och storleken på de kortsiktiga svängningarna, kommer att minska, medan den trenden etablerar sig hos handlarna.

För det tredje: Att känna igen cykler i volatiliteten, kan vara användbart för att fastställa lämpliga tidpunkter då ett utbrott kan förväntas. Många aktier har cykler med en hög grad av regelbundenhet. När det gäller volatilitet, så har den en tendens till att fortsätta i samma riktning som vändningen påbörjat.

Slutligen: Volatilitet kan användas för att beräkna det teoretiska värdet på optioner.

Volatilitet modellen i Vikingen

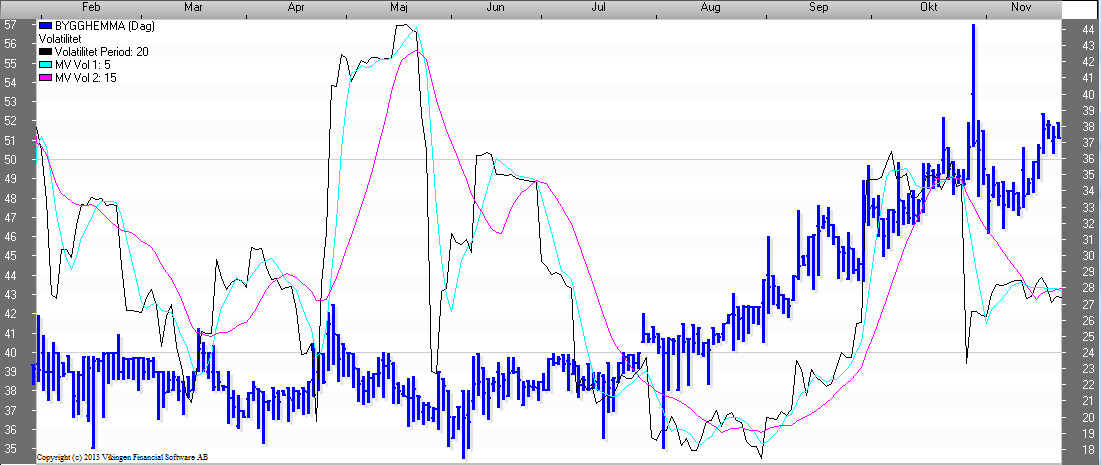
Denna modell visar den årliga historiska volatiliteten under “Period” perioder.

Volatilitet mäter förändringar i kursens svängningar. Det är ett medeltal av det absoluta förändringarna.
Med Volatilitetsmodellen är det möjligt att beräkna storleken på de små svängningarna i kursen.

Använd denna modell för att spåra upp onormalt stora kurssvängningar för ett objekt.
Volatilitetsmodellen kan även användas för att skaffa sig en uppfattning om de mycket korta svängningarna.