Fibonacci

Har du noen gang hørt om Fibonacci-sekvensen? Eller det gylne snitt? Eller den gylne spiral?

Disse mystiske tallene og formene er alle knyttet til hverandre. Hvis du ser nøye etter, kan de bli funnet på de mest uventede stedene, og skape vakre og tiltalende mønstre.

Enkelt sagt er Fibonacci-sekvensen en serie tall som starter med 1 og 1. Derfra legger du til de to foregående tallene i sekvensen for å få det neste tallet. Dette er en type rekursiv sekvens.

Så 1+1=2, 1+2=3, 2+3=5 og så videre. Dette gir deg en sekvens som ser ut som 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etc. Men hva gjør denne sekvensen så spesiell og interessant?

Den matematiske sekvensen som styrer naturen

For det første kan Fibonacci-tall finnes i den naturlige verden rundt oss. For eksempel vil de fleste blomster ha et antall kronblader som tilsvarer Fibonacci-sekvensen. Iris har tre kronblad mens ville roser og ranunkler har fem kronblad. Det er selvfølgelig helt til et kronblad faller av. Ikke rart at sjeldne firkløver anses som heldige!

Hvis du skjærer i et stykke frukt, vil du sannsynligvis finne et Fibonacci-nummer der også, slik frøseksjonene er ordnet. Bananer har tre deler mens epler har fem.

Fibonacci-sekvensen spiller til og med en rolle i de subtile spiralene du kan se i frøhodet til en solsikke. Dette skyldes noe som kalles det gylne snitt, det gyldne snitt eller den greske bokstaven Phi. Hvis du tar et tall i rekkefølgen over 5, og deler det på det forrige tallet, får du et svar svært nær 1,618. Jo større tallene er, desto nærmere kommer du 1,618. Det gylne snitt er et irrasjonelt tall, og kan derfor ikke skrives som en brøk. Igjen, dette er et tall som kan finnes i den naturlige verden.

Ta solsikken. For å være så effektive som mulig, må frøene pakkes tett uten å overlappe. Nå, hvis det bare vokste frø i en rett linje i én retning, ville det etterlatt mye tomt på blomsterhodet. Den beste måten å minimere bortkastet plass på er at frøene vokser i spiraler, med hvert frø som vokser i en liten vinkel vekk fra det forrige.

Hvis graden av sving var en brøkdel, som 1/4, så spiller det ingen rolle fordi etter fire omdreininger ville frømønsteret være tilbake til begynnelsen igjen. Det ville være fire rader med frø, men det er ikke mye bedre enn én når du prøver å dekke et sirkulært område. Den perfekte graden av flaks må være et irrasjonelt tall, ikke lett tilnærmet med en brøk, og svaret er det gylne snitt.

Fibonacci-spiralen finnes i kunst, arkitektur, biologi og mange flere steder

Gjør tall til en iøynefallende spiral

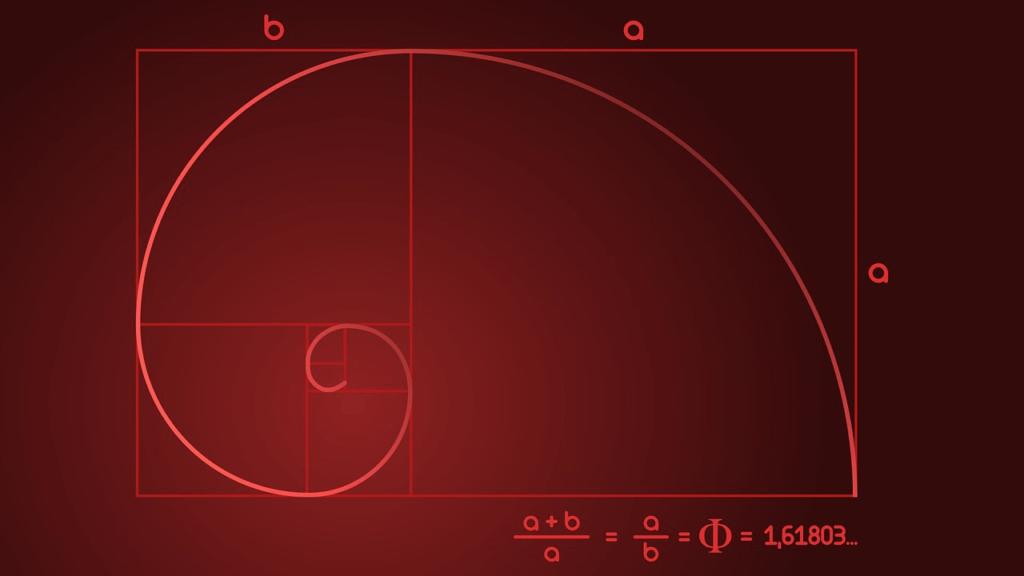
En annen måte å tenke på det gylne snitt på er som en spiral. Denne spiralen utvides med en faktor på 1,618 hver gang den gjør en kvart sving (90°).

Å tegne en perfekt gylden spiral er ganske vanskelig å gjøre for hånd, men som med det gylne snitt, kan du få en nær tilnærming med Fibonacci-spiralen. Dette lages ved å tegne en bue gjennom en rekke kvadrater som tilsvarer Fibonacci-tallene, så 1², 1², 2², 3² osv.

Du har kanskje sett disse spiralene lagt over kjente kunstverk, mens eksperter prøver å forklare hvorfor vi finner dem så estetisk tiltalende. Ofte trekker spiralen blikket vårt slik at fokuset til kunstverket finnes i midten av spiralen. Eksempler finnes i verkene til Leonardo da Vinci og Salvador Dali.

Lytt etter Fibonacci-sekvensen i musikk

Fibonacci oppdaget faktisk ikke sekvensen selv. Matematikeren ble født Leonardo Bonacci i Pisa på 1100-tallet, Italia, og reiste mye rundt i Nord-Afrika. Der lærte han hvordan de hindu-arabiske tallene 0-9 kunne brukes til å gjøre beregninger enklere enn de romerske tallene som fortsatt brukes i store deler av Europa. Fibonacci forklarte oppdagelsene sine i en bok kalt Liber Abaci, utgitt i 1202, som hadde en del viet til den spennende sekvensen som ville bli oppkalt etter ham hundrevis av år senere.

Imidlertid hadde indiske poeter og musikere allerede vært klar over Fibonacci-sekvensen i århundrer, etter å ha oppdaget dens implikasjoner for rytme og forskjellige kombinasjoner av lange og korte beats.

Mozart brukte det gylne snitt når han skrev en rekke av sine pianosonater. En sonate kan deles inn i to separate seksjoner, kjent som utstillingen (hvor temaet introduseres) og utviklingen og rekapitulasjonen (hvor temaet utvikles og gjentas). I Mozarts sonater er antall takter i siste del delt på førstnevnte omtrent 1,618, det gylne snitt.

Det er til og med en poesistil inspirert av Fibonacci-sekvensen, kjent som Fib Poetry. Hver linje i diktet må inneholde det nøyaktige antallet stavelser som tilsvarer Fibonacci-sekvensen. Så et sekslinjers dikt ville ha stavelseslinjer på 1, 1, 2, 3, 5 og 8.

Om vikingen

Med Vikings signaler har du god sjanse til å finne vinnerne og selge i tide. Det er mange verdipapirer. Med Vikings autopiloter, prisdata, tabeller og aksjekurser kan du sortere ut de mest interessante ETFene, aksjene, opsjonene, warrantene, fondene m.m.

Klikk her for å se hva Vikingen tilbyr: Detaljert sammenligning – Børsprogram for de som ønsker å bli enda rikere (vikingen.se)