Fibonacci

Har du nogensinde hørt om Fibonacci-sekvensen? Eller det gyldne snit? Eller den gyldne spiral?

Disse mystiske tal og former er alle forbundet med hinanden. Hvis man ser godt efter, kan de findes på de mest uventede steder og skabe smukke og tiltalende mønstre.

Kort sagt er Fibonacci-rækken en række tal, der starter med 1 og 1. Derfra lægges de to foregående tal i rækken sammen for at få det næste tal. Dette er en form for rekursiv sekvens.

Så 1+1=2, 1+2=3, 2+3=5 og så videre. Dette giver dig en sekvens, der ser ud som 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 osv. Men hvad gør denne sekvens så speciel og interessant?

Den matematiske rækkefølge, der styrer naturen

For det første kan Fibonacci-tal findes i den naturlige verden omkring os. For eksempel vil de fleste blomster have et antal kronblade, der svarer til Fibonacci-sekvensen. Iris har tre kronblade, mens vilde roser og smørblomster har fem kronblade. Det vil sige, indtil et kronblad falder af. Ikke underligt, at sjældne firkløvere betragtes som heldige!

Hvis du skærer i et stykke frugt, vil du sandsynligvis også finde et Fibonacci-tal i den måde, kernerne er arrangeret på. Bananer har tre dele, mens æbler har fem.

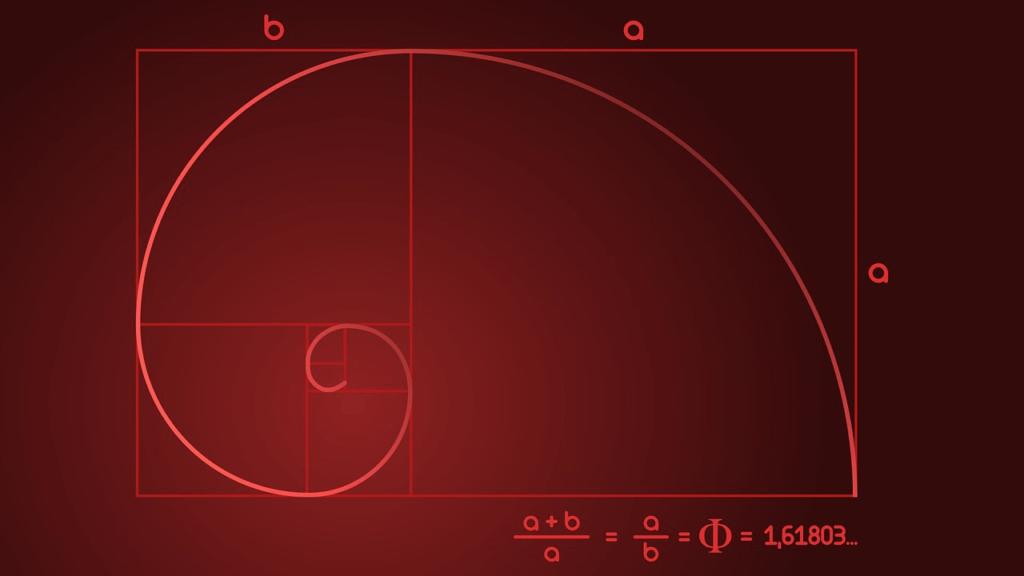
Fibonacci-sekvensen spiller endda en rolle i de subtile spiraler, man kan se i frøhovedet på en solsikke. Det skyldes noget, der kaldes det gyldne snit, det gyldne forhold eller det græske bogstav Phi. Hvis man tager et tal i rækken over 5 og dividerer det med det foregående tal, får man et svar, der er meget tæt på 1,618. Jo større tallene er, jo tættere kommer du på 1,618. Det gyldne snit er et irrationelt tal og kan derfor ikke skrives som et brøktal. Igen er dette et tal, der kan findes i den naturlige verden.

Tag solsikken. For at være så effektiv som muligt skal dens frø pakkes tæt sammen uden at overlappe hinanden. Hvis den nu kun groede frø i en lige linje i én retning, ville det efterlade masser af tom plads på blomsterhovedet. Den bedste måde at minimere spild af plads på er at lade frøene vokse i spiraler, hvor hvert frø vokser i en lille vinkel væk fra det foregående.

Hvis drejningsgraden var en brøkdel, f.eks. 1/4, ville det være ligegyldigt, for efter fire omgange ville seed-mønsteret være tilbage ved begyndelsen igen. Der ville være fire rækker af frø, men det er ikke meget bedre end én, når man forsøger at dække et cirkulært område. Den perfekte grad af held må være et irrationelt tal, som ikke let kan tilnærmes med en brøk, og svaret er det gyldne snit.

Fibonacci-spiralen kan findes i kunst, arkitektur, biologi og mange andre steder.

Forvandling af tal til en iøjnefaldende spiral

En anden måde at tænke på det gyldne snit er som en spiral. Denne spiral bliver bredere med en faktor på 1,618, hver gang den drejer en kvart omgang (90°).

Det er ret svært at tegne en perfekt gylden spiral i hånden, men ligesom med det gyldne snit kan du få en god tilnærmelse med Fibonacci-spiralen. Den skabes ved at tegne en bue gennem en række firkanter, der svarer til Fibonacci-tallene, altså 1², 1², 2², 3² osv.

Du har måske set disse spiraler overlejret på berømte kunstværker, mens eksperter forsøger at forklare, hvorfor vi finder dem så æstetisk tiltalende. Ofte trækker spiralen vores øjne til sig, så kunstværkets fokus er i spiralens centrum. Eksempler er værker af Leonardo da Vinci og Salvador Dali.

Lyt efter Fibonacci-sekvensen i musikken

Fibonacci opdagede faktisk ikke selv sekvensen. Leonardo Bonacci blev født i det 12. århundredes Pisa i Italien, og matematikeren rejste meget rundt i Nordafrika. Der lærte han, hvordan de hindu-arabiske tal 0-9 kunne bruges til at gøre udregninger lettere end de romertal, der stadig bruges i store dele af Europa. Fibonacci forklarede sine opdagelser i en bog ved navn Liber Abaci, der blev udgivet i 1202, og som havde et afsnit dedikeret til den spændende sekvens, der skulle blive opkaldt efter ham flere hundrede år senere.

Indiske digtere og musikere havde dog allerede været opmærksomme på Fibonacci-sekvensen i århundreder og havde opdaget dens implikationer for rytme og forskellige kombinationer af lange og korte slag.

Mozart brugte det gyldne snit, da han skrev en række af sine klaversonater. En sonate kan opdeles i to separate sektioner, kendt som ekspositionen (hvor temaet introduceres) og udviklingen og rekapitulationen (hvor temaet udvikles og gentages). I Mozarts sonater er antallet af takter i den sidste del divideret med den første omkring 1,618, det gyldne snit.

Der findes endda en digtstil, der er inspireret af Fibonacci-sekvensen, kendt som Fib Poetry. Hver linje i digtet skal indeholde præcis det antal stavelser, der svarer til Fibonacci-rækken. Så et digt på seks linjer ville have stavelseslinjer på 1, 1, 2, 3, 5 og 8.

Om vikingen

Med Viking’s signaler har du en god chance for at finde vinderne og sælge i tide. Der findes mange værdipapirer. Med Vikings autopiloter, prisdata, tabeller og aktiekurser kan du sortere de mest interessante ETF’er, aktier, optioner, warrants, fonde osv. fra.

Klik her for at se, hvad Vikingen tilbyder: Detaljeret sammenligning – Børsprogram for dig, der vil blive endnu rigere (vikingen.se)