Fibonacci

Har du någonsin hört talas om Fibonacci-sekvensen? Eller det gyllene snittet? Eller den gyllene spiralen?

Dessa mystiska siffror och former är alla kopplade till varandra. Om du tittar noga kan de hittas på de mest oväntade platserna, vilket skapar vackra och tilltalande mönster.

Enkelt uttryckt är Fibonacci-sekvensen en serie siffror som börjar med 1 och 1. Därifrån lägger du ihop de två föregående talen i sekvensen för att få nästa nummer. Detta är en typ av rekursiv sekvens.

Alltså 1+1=2, 1+2=3, 2+3=5 och så vidare. Detta ger dig en sekvens som ser ut som 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 etc. Men vad gör den här sekvensen så speciell och intressant?

Den matematiska sekvensen som styr naturen

Till att börja med kan Fibonacci-tal hittas i den naturliga världen runt omkring oss. De flesta blommor kommer till exempel att ha ett antal kronblad som motsvarar Fibonacci-sekvensen. Iris har tre kronblad medan vildrosor och smörblommor har fem kronblad. Det är naturligtvis tills ett kronblad faller av. Inte konstigt att sällsynta fyrklöver ses som tur!

Om du skär i en bit frukt kommer du sannolikt att hitta ett Fibonacci-nummer där också, i hur frönas sektioner är ordnade. Bananer har tre delar medan äpplen har fem.

Fibonacci-sekvensen spelar till och med en roll i de subtila spiralerna du kan se i fröhuvudet på en solros. Detta beror på något som kallas det gyllene snittet, det gyllene snittet eller den grekiska bokstaven Phi. Om du tar ett tal i sekvensen över 5, och dividerar det med det föregående talet, får du ett svar mycket nära 1,618. Ju större siffror, desto närmare 1,618 kommer du. Det gyllene snittet är ett irrationellt tal, och kan därför inte skrivas som ett bråktal. Återigen, detta är ett nummer som kan hittas i den naturliga världen.

Ta solrosen. För att vara så effektiva som möjligt måste dess frön packas tätt ihop utan att överlappa varandra. Nu, om det bara växte frön i en rak linje i en riktning, skulle det lämna massor av tomt utrymme på blomhuvudet. Det bästa sättet att minimera slöseri med utrymme är att fröna växer i spiraler, där varje frö växer i en liten vinkel bort från det föregående.

Om graden av sväng var en bråkdel, som 1/4, så spelar det ingen roll eftersom efter fyra varv skulle frömönstret vara tillbaka i början igen. Det skulle finnas fyra rader med frön, men det är inte mycket bättre än en när man försöker täcka ett cirkulärt område. Den perfekta graden av tur måste vara ett irrationellt tal, som inte lätt kan approximeras med en bråkdel, och svaret är det gyllene snittet.

Fibonacci-spiralen kan hittas inom konst, arkitektur, biologi och många fler platser

Förvandlar siffror till en iögonfallande spiral

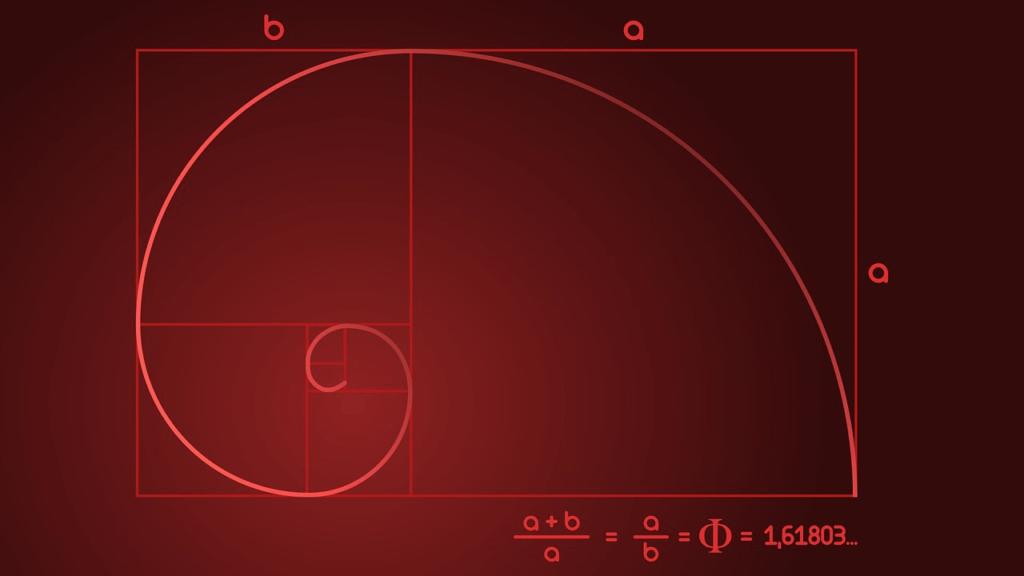
Ett annat sätt att tänka på det gyllene snittet är som en spiral. Denna spiral blir bredare med en faktor 1,618 varje gång den gör ett kvarts varv (90°).

Att rita en perfekt gyllene spiral är ganska knepigt att göra för hand, men precis som med det gyllene snittet kan du få en nära approximation med Fibonacci-spiralen. Detta skapas genom att dra en båge genom en serie kvadrater som motsvarar Fibonacci-talen, så 1², 1², 2², 3² etc.

Du kanske har sett dessa spiraler överlagrade över kända konstverk, eftersom experter försöker förklara varför vi tycker att de är så estetiskt tilltalande. Ofta drar spiralen i vårt öga så att konstverkets fokus återfinns i mitten av spiralen. Exempel finns i verk av Leonardo da Vinci och Salvador Dali.

Lyssna efter Fibonacci-sekvensen i musik

Fibonacci upptäckte faktiskt inte sekvensen själv. Född Leonardo Bonacci i 1100-talets Pisa, Italien, reste matematikern mycket runt Nordafrika. Där lärde han sig hur de hindu-arabiska siffrorna 0-9 kunde användas för att göra beräkningar lättare än de romerska siffrorna som fortfarande används i stora delar av Europa. Fibonacci förklarade sina upptäckter i en bok som heter Liber Abaci, publicerad 1202, som hade ett avsnitt ägnat åt den spännande sekvens som skulle döpas efter honom hundratals år senare.

Indiska poeter och musiker hade dock redan varit medvetna om Fibonacci-sekvensen i århundraden, efter att ha upptäckt dess implikationer för rytm och olika kombinationer av långa och korta beats.

Mozart använde sig av det gyllene snittet när han skrev ett antal av sina pianosonater. En sonat kan delas in i två separata avsnitt, kända som expositionen (där temat introduceras) och utvecklingen och rekapituleringen (där temat utvecklas och upprepas). I Mozarts sonater är antalet takter i den senare delen dividerat med den förra cirka 1,618, det gyllene snittet.

Det finns till och med en poesistil inspirerad av Fibonacci-sekvensen, känd som Fib Poetry. Varje rad i dikten måste innehålla det exakta antalet stavelser som motsvarar Fibonacci-sekvensen. Så en sexradsdikt skulle ha stavelserader på 1, 1, 2, 3, 5 och 8.

Om Vikingen

Med Vikings signaler har du en god chans att hitta vinnarna och sälja i tid. Det finns många värdepapper. Med Vikings autopiloter, kursdata, tabeller och börskurser kan du sortera ut de mest intressanta ETFerna, aktierna, optionerna, warranterna, fonderna osv.

Klicka här för att se vad Vikingen erbjuder: Detaljerad jämförelse – Börsprogram för dem som vill bli ännu rikare (vikingen.se)